中古マンション売買データを分析してみた(3) - (より妥当なモデル化をした)路線と駅による中古売買価格推定
いくつかテクニカルに試行錯誤したり,他のことをやってたりしてしばらく間があいてしまいましたが,ようやく前回やった路線と駅モデルの精度向上ができました.エントリの最後に書いた通り,以前の路線・駅による中古マンション売買価格モデルは,大きな問題を抱えていました.
で,それならモデルに両変数を組み込めばいいじゃないか,という話なのですが,駅からの距離と築年数をモデルに組み込むと,まともな値がかえってこない状態になってしまっています.特に築年数に関しては,平米単価との単相関が0.7以上あるにも関わらず,前回の記事でお見せしたように,1990年代以降に傾きが大きくあがり,実は非線形の関係にあります.このあたりをうまくモデルに組み込まないと,まともな推定違えられないように考えています.なので引き続きこのあたりを再検討したいところです.
ということで,今まで使っていたBUGSからStanに乗り換えて,ベイズ推定についてもいくつか学びなおして,ようやくまともな結果が得られたので,今回はそのご紹介をできればと思います*1.
モデル
基本的には,前回と前々回のモデルを組み合わせた形になります.通常の線形回帰に,駅と路線を追加した形になります*2.
これを数式で表すと以下のようになります.
ここでは物件,
は駅,
は路線を表します.
は,それぞれひとつの
と
に所属するという形の階層ベイズモデルになります*3.
ちなみに前回のモデルも同様に書き表すと,以下のようになります.物件レベルの変数がいっさいないということですね.
そして今回のモデルをStanに落としたコードが以下のようになります.
data { int<lower=1> N; # sample num int<lower=1> M; # independents' num int<lower=1> N_T; # train num int<lower=1> N_S; # station num matrix[N, M] X; # independents vector[N] Y; # dependent int<lower=1, upper=N_T> T[N]; # train int<lower=1, upper=N_S> S[N]; # station } parameters { real a; vector[M] b; real r_t[N_T]; real r_s[N_S]; real<lower=0> s; real<lower=0> s_rs; real<lower=0> s_rt; } model { # regresion model with random effect for (i in 1:N) Y[i] ~ normal(a+X[i]*b+r_t[T[i]]+r_s[S[i]], s); # prior distributions s ~ uniform(0, 1.0e+4); a ~ normal(39, 1.0e+4); for (i in 1:M) b[i] ~ normal(0, 1.0e+4); for (i in 1:N_T) r_t[i] ~ normal(0, s_rt); for (i in 1:N_S) r_s[i] ~ normal(0, s_rs); # hierarchical prior distribution s_rt ~ uniform(0, 1.0e+4); s_rs ~ uniform(0, 1.0e+4); }
路線・駅を入れたことによる住宅レベル変数の推定値変化
今回のモデルは,第1回の線形モデルに路線および駅の項を追加したものです.この追加によって,築年,駅からの距離などの効果がどうなったをグラフに表したのが下の図です.黒丸がlm()で普通の線形回帰を行ったときの偏回帰係数,そして分布が今回の推定で得られたものです*4.
路線と駅を入れたことにより,部屋数や床面積の係数が小さくなっています.この場合は「係数が小さくなる=価格に及ぼす影響が小さくなった」ととらえることが可能です.部屋数や床面積の効果とみられていたもののいくらかは,路線と駅によるみせかけの効果だったと考えられます.
その一方で築年の効果はほぼ変化がなく*5,駅からの距離に至ってはむしろ係数が大きくなっています.これは,前回の考察部分で問題として取り上げたように,あざみ野や新百合ケ丘のような,駅から遠いところに高級住宅地が固まっているような地域のせいで駅からの距離の効果が過小推定されていたと考えられます.
路線の効果
さて,ここからは前回との比較をしていきます.前回と今回の結果は,それぞれ以下の通りになります.グラフの形式が微妙にそろっていないのはご容赦ください...
| 前回 | 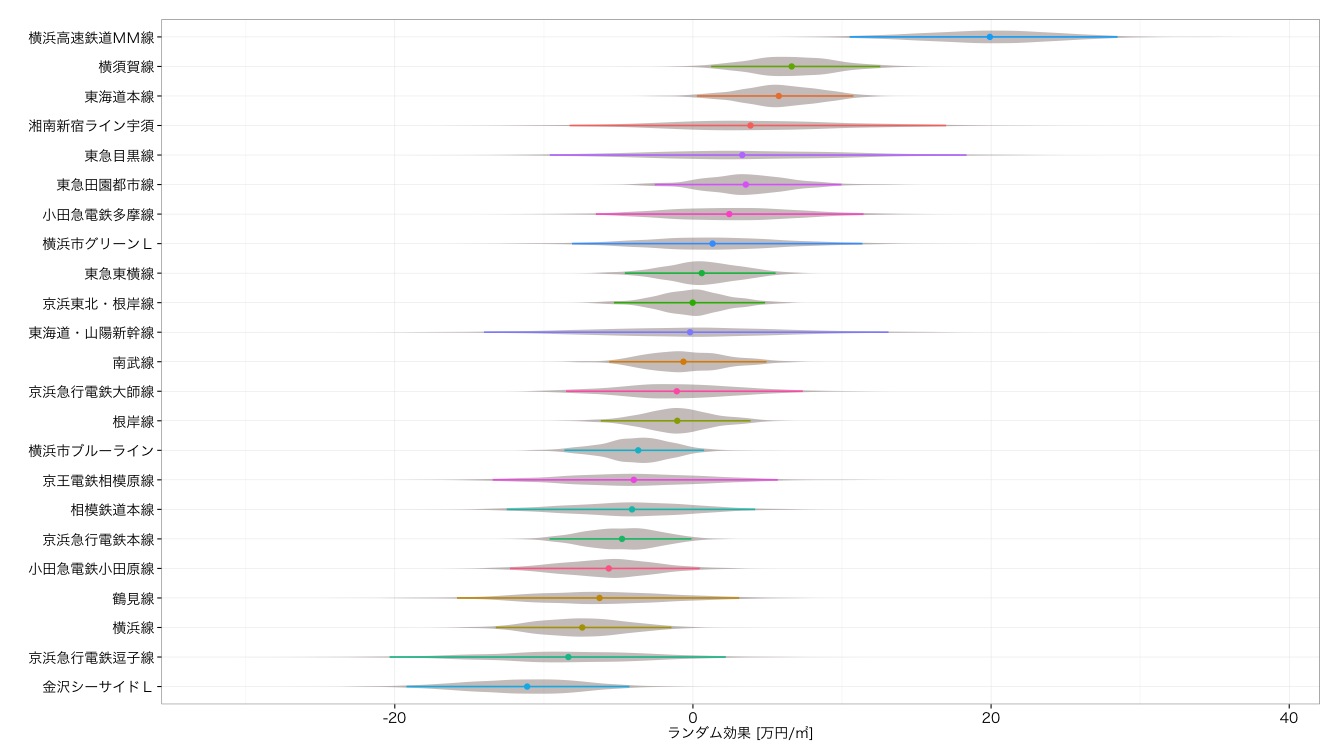 |
| 今回 | 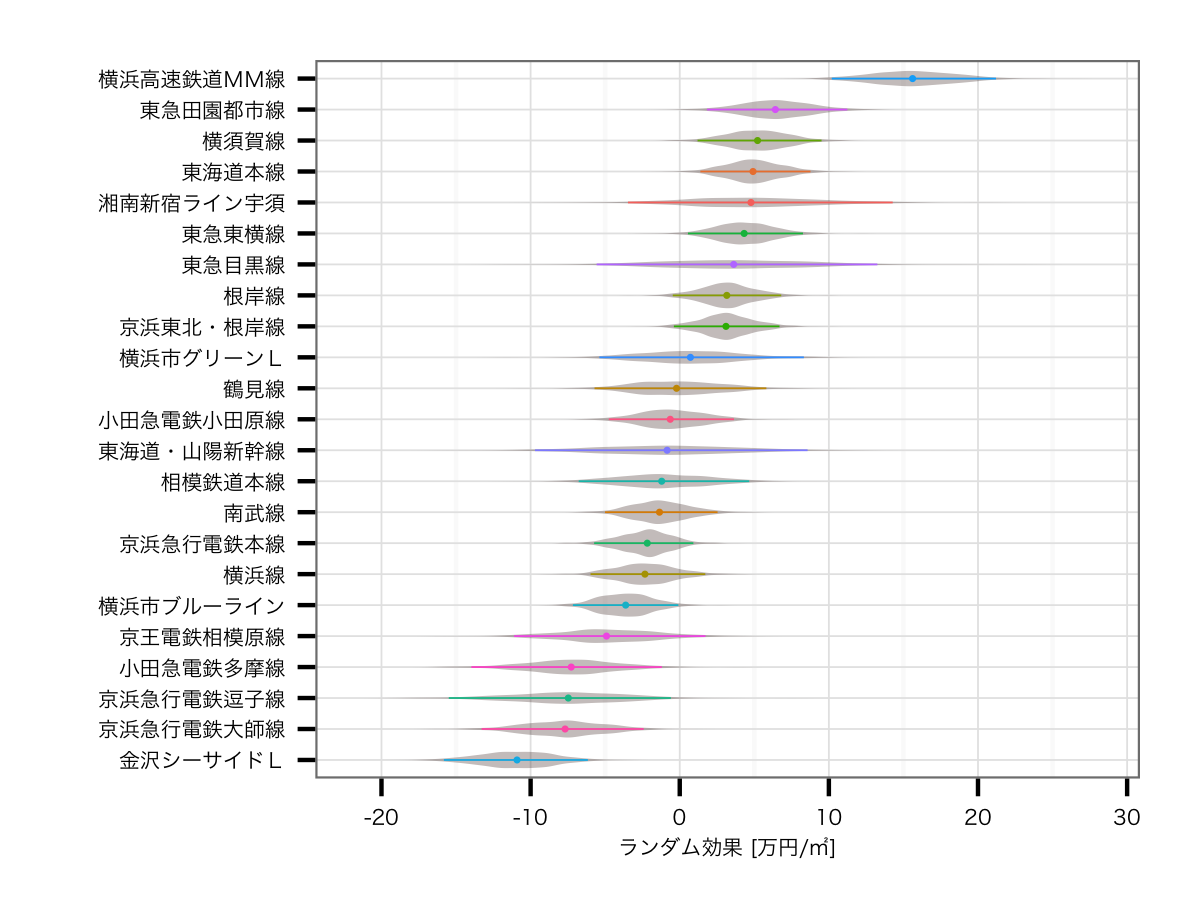 |
全体としてそこまで大きな違いがあるわけではないですが,東急田園都市線が6位から2位に上昇していたり,逆に京急大師線が中段グループから,下からに2番目まで落ちていたりといった違いがあります.これらは基本的に,売買された中古住宅の,路線毎の特性が影響したものと考えられます.
京急大師線のあたりは,再開発等により駅近のマンションが割と多かったり,再開発でタワーマンションが建てられていることによるものと考えられます.東急田園都市線は逆にあざみ野やたまプラーザといった,典型的な車で生活するタイプの高級住宅地を抱えており,前回の分析では実際の価値より低く見えてしまっていたということになります*6.
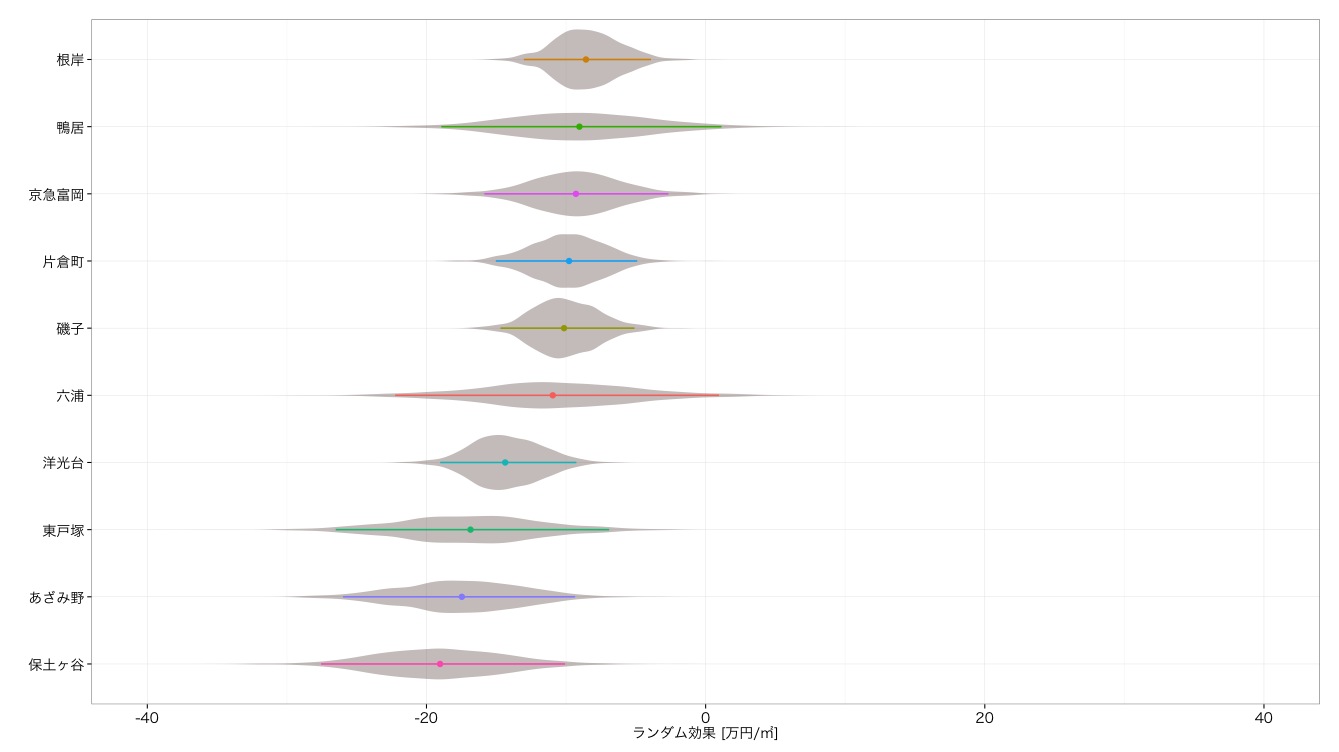
駅の効果
トップ10
これも同じように,前回と今回の比較を行っていきたいと思います.まずはトップ10から.
| 前回 | 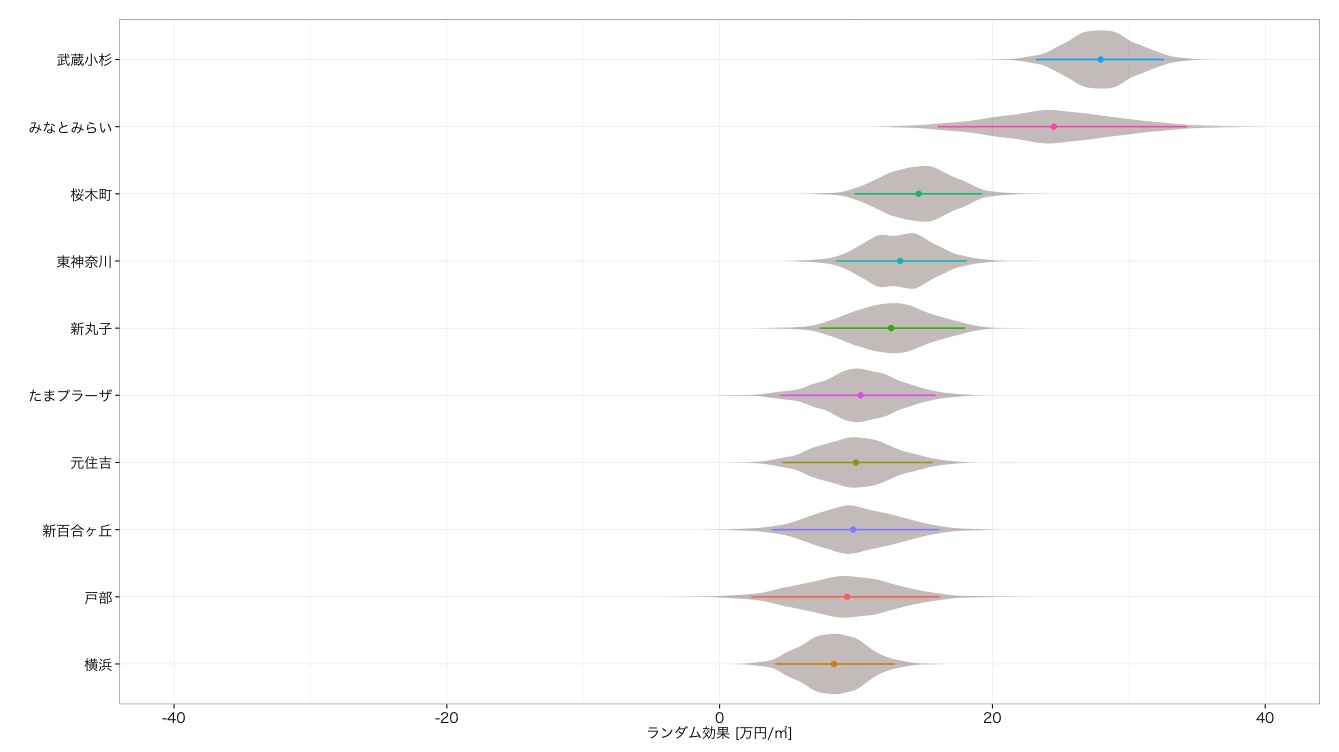 |
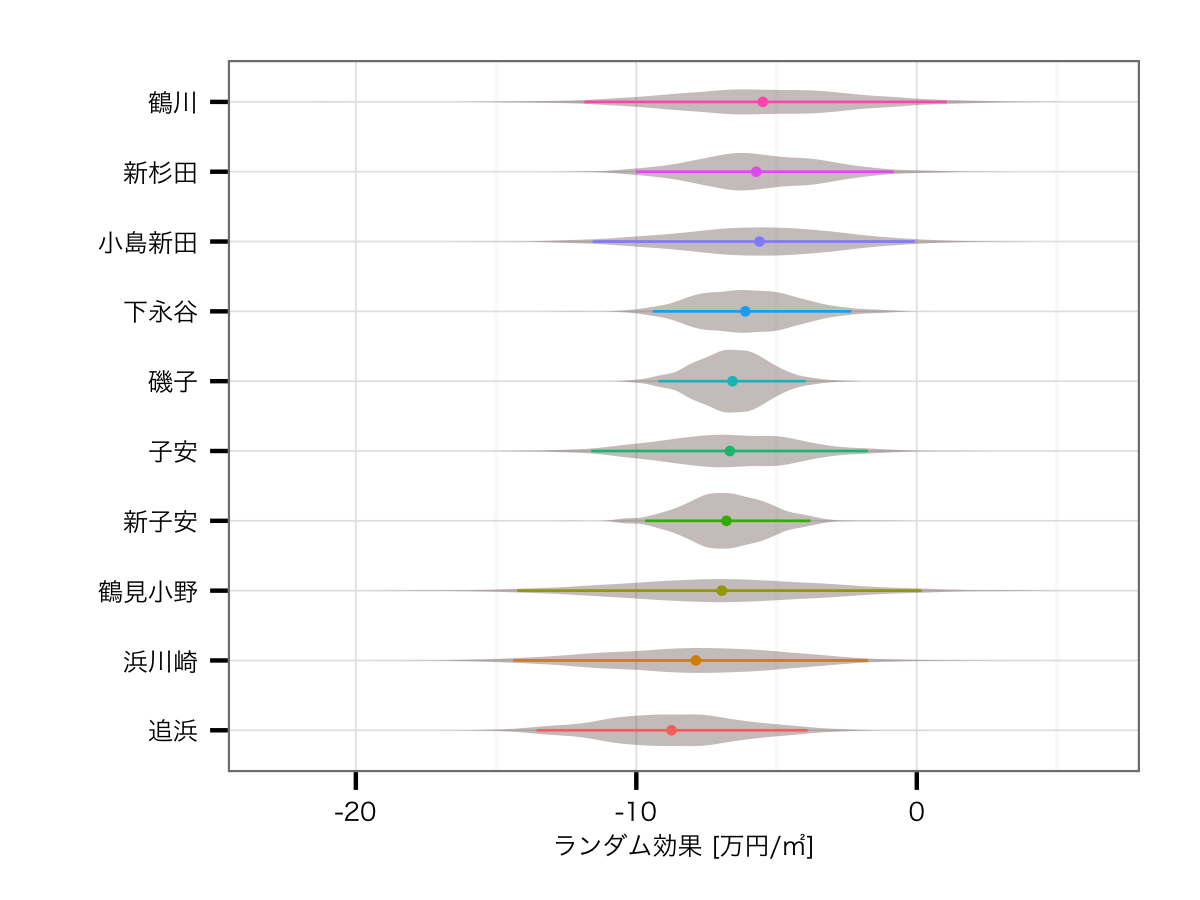
| 今回 |  |
まず効果の大きさをみていただくと,全体的に効果が減少しているのが見て取れるかと思います.特に2ヘッドの武蔵小杉とみなとみらいは,10万円以上効果が落ちています.どちらも駅近にタワーマンションが密集しているエリアのため,元々の効果が過大推定されていたわけです.しかし効果が落ちてもなお他の駅より頭一つ抜けているわけですが... そして,小田急線の誇る閑静な高級住宅地である新百合ケ丘が,8位から3位に躍進しています*7.鹿島田なども同様に,駅から距離のある場所に古くからある住宅街や商店街といった町並みの所為だと考えられます.
そんなわけで
2ヶ月近く時間が経ってしまいましたが,前回の無念をようやくはらせました.さらにこのモデルを発展させるかはまだ考え中ですが,もし続けるとしたら,路線毎,駅毎の駅からの距離 or 築年による価格下落モデルを階層ベイズモデルでするとかですかね...
*1:コードはgithubにあげてあるので,そちらを参照ください.
*2:なお,テクニカルな方のエントリで書いた通り,個体差を入れたモデルでは,ほぼ線形モデルの推定値には変化はありませんでした.推定するパラメタも増えて計算時間もかかり,モデル自体の安定性も下がると思われるので,今回のモデルでは個体差項は含まない形でモデルを組みました.
*3:ここで当然,駅は路線に包含されるのだから,さらに階層を重ねた形のモデルにするべきだという意見をお持ちの方もいるかもしれません.しかし実際には,ひとつの駅が複数の路線に所属することがある(たとえば横浜駅には合計12路線が乗り入れています)ため,単純な2段階の階層モデルにすることはできません.そのためデータベースから取ってきた段階で,物件毎に最寄り駅と最寄り路線が割り当てられているため,ここではそれを正として,こちら側で特に加工しないことにしました.これは,物件データベースにあるもの=不動産屋が最も価値があると判断した最寄り路線と最寄り駅,だと暗黙のうちに考えられるからです.例えば横浜駅が最寄りのときに,JR東海道線や東急東横線が最寄りだという書き方はしても,相鉄線やブルーラインが最寄りだと書くことはほぼありえないでしょう.
*4:lm()だと平均値+95%信頼区間しか得られず,(もちろんboxplotなどで信頼区間を表すことはできますが,)分布形状を表すことができません.Stanだと分布形状まで得ることが可能なので,このような点と分布の比較になっています.
*5:余談ですが,築年の分布は極めて幅が狭くなっており,これは築年数に応じて,ブレなく線形に価格が下落していくことを示しています.
*6:東急田園都市線は,東急電鉄によって1960-80年代に開発された多摩田園都市を抱えており,梶ヶ谷-中央林間の物件は駅から遠く,また築年数もそれなりになってきていると考えられます.
*7:一回新百合ケ丘にいって歩き回ってみるとわかりますが,駅近辺はショッピングモールなどしかなく,10分弱歩かないと住宅街に到達しません.そして車でないといけない距離に山ほどの高級住宅が点在しています.
*8:ちなみに今回のモデルでの効果は133駅中29位で,ランダム効果は+2.7万円と感覚的に納得できる結果になりました.