glmnetで正則化を試してみる
タイトルの通り,よく考えたら今までL1/L2正則化を知識としては知ってるけど,実際に試したことはなかったことに気がついたので試してみましたよという話.L1/L2正則化にの理屈については,TJOさんのエントリとか,unnounnoさんのエントリとかをみてもらえれば良いのではと思います.それより詳しいことが知りたければ,PRMLでも読めば良いのではないでしょうか(適当*1).
まずはデータを眺める
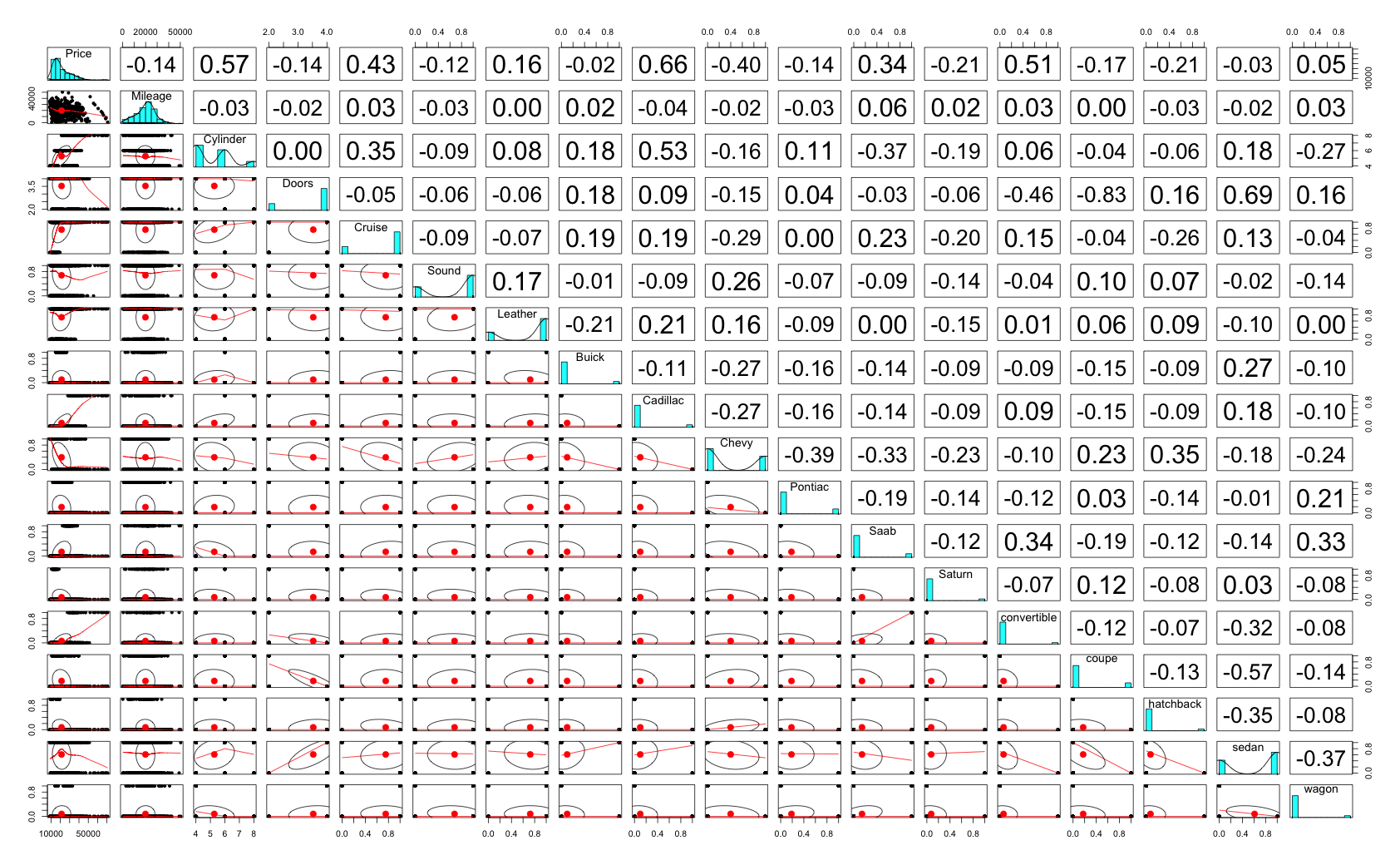
使用したデータは,caretパッケージのcarsパッケージです*2.中古車販売のデータっぽくて,価格と,走行距離とか気筒とかドア数とかの車に関するカラムが並んでます.データを読み込んで,可視化して,とりあえず lm() してみます.
> library(glmnet) > library(caret) > library(psych) > > # load data > data(cars) > t(head(cars)) 1 2 3 4 5 6 Price 22661.05 21725.01 29142.71 30731.94 33358.77 30315.17 Mileage 20105.00 13457.00 31655.00 22479.00 17590.00 23635.00 Cylinder 6.00 6.00 4.00 4.00 4.00 4.00 Doors 4.00 2.00 2.00 2.00 2.00 2.00 Cruise 1.00 1.00 1.00 1.00 1.00 1.00 Sound 0.00 1.00 1.00 0.00 1.00 0.00 Leather 0.00 0.00 1.00 0.00 1.00 0.00 Buick 1.00 0.00 0.00 0.00 0.00 0.00 Cadillac 0.00 0.00 0.00 0.00 0.00 0.00 Chevy 0.00 1.00 0.00 0.00 0.00 0.00 Pontiac 0.00 0.00 0.00 0.00 0.00 0.00 Saab 0.00 0.00 1.00 1.00 1.00 1.00 Saturn 0.00 0.00 0.00 0.00 0.00 0.00 convertible 0.00 0.00 1.00 1.00 1.00 1.00 coupe 0.00 1.00 0.00 0.00 0.00 0.00 hatchback 0.00 0.00 0.00 0.00 0.00 0.00 sedan 1.00 0.00 0.00 0.00 0.00 0.00 wagon 0.00 0.00 0.00 0.00 0.00 0.00 > pairs.panels(cars) > > # lm > fit.lm <- glm(Price ~ ., data = cars) > summary(fit.lm) Call: glm(formula = Price ~ ., data = cars) Deviance Residuals: Min 1Q Median 3Q Max -9513.5 -1540.9 125.4 1470.3 13619.7 Coefficients: (3 not defined because of singularities) Estimate Std. Error t value Pr(>|t|) (Intercept) -1.124e+03 9.926e+02 -1.133 0.25773 Mileage -1.842e-01 1.256e-02 -14.664 < 2e-16 *** Cylinder 3.659e+03 1.133e+02 32.286 < 2e-16 *** Doors 1.567e+03 2.589e+02 6.052 2.2e-09 *** Cruise 3.409e+02 2.960e+02 1.152 0.24978 Sound 4.409e+02 2.345e+02 1.880 0.06043 . Leather 7.908e+02 2.497e+02 3.167 0.00160 ** Buick 9.477e+02 5.525e+02 1.715 0.08670 . Cadillac 1.336e+04 6.248e+02 21.386 < 2e-16 *** Chevy -5.492e+02 4.397e+02 -1.249 0.21203 Pontiac -1.400e+03 4.868e+02 -2.875 0.00414 ** Saab 1.228e+04 5.546e+02 22.139 < 2e-16 *** Saturn NA NA NA NA convertible 1.102e+04 5.419e+02 20.340 < 2e-16 *** coupe NA NA NA NA hatchback -6.362e+03 6.104e+02 -10.422 < 2e-16 *** sedan -4.449e+03 4.463e+02 -9.969 < 2e-16 *** wagon NA NA NA NA --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for gaussian family taken to be 8445957) Null deviance: 7.8461e+10 on 803 degrees of freedom Residual deviance: 6.6639e+09 on 789 degrees of freedom AIC: 15122 Number of Fisher Scoring iterations: 2
相関は各変数そこそこある感じで,極端に高いものはないみたいです.でもlm()の結果をみると,Saturnとcoupeとwagonは落ちちゃってますね.まぁその辺りは気にせず次へ.
glmnetでL1正則化
Rで正則化をするパッケージとして {glmnet} を使います.読み込みにfactor型は使えず,すべて数値型で渡す必要があります.かつYとXは別のmatrixとして渡してあげる必要があるとのこと.実行して,plotしてみます.式中の alpha が1ならL1正則化で,0ならL2正則化になります.そしてその間ならElastic Netです.
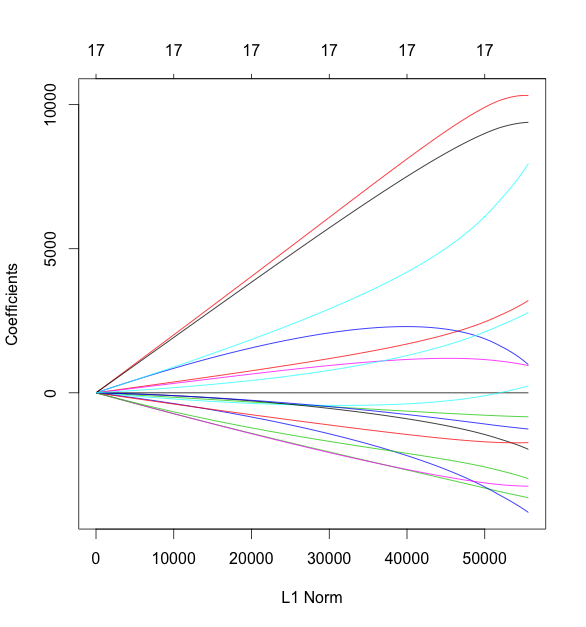
> pairs.panels(cars) > # lasso > fit.glmnet.lasso <- glmnet(as.matrix(cars[, -1]), + as.matrix(cars[, 1]), + alpha = 1) > plot(fit.glmnet.lasso)
この図は,左にいくほどL1正則化が強く効いている状態とのことです.さらに cv.glmnet() で5 foldのクロスバリデーションを行います.
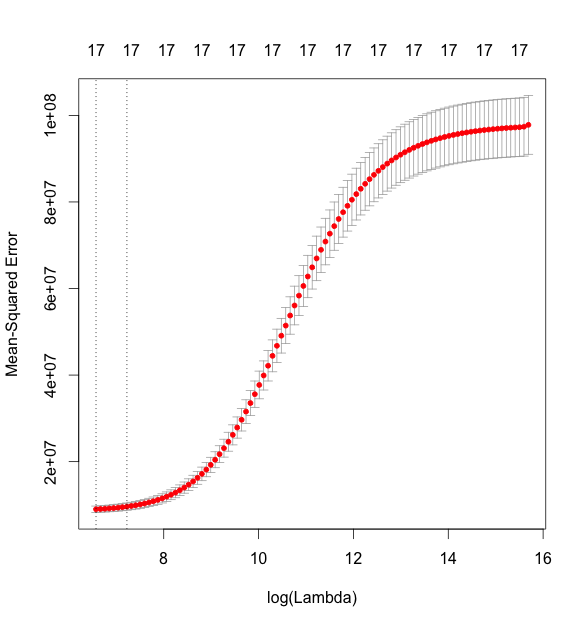
> fit.glmnet.lasso.cv <- cv.glmnet(as.matrix(cars[, -1]), + as.matrix(cars[, 1]), + nfold = 5, + alpha = 1) > plot(fit.glmnet.lasso.cv) > fit.glmnet.lasso.cv$lambda.min [1] 18.54925 > fit.glmnet.lasso.cv$lambda.1se [1] 275.4505 > coef(fit.glmnet.lasso.cv, s = fit.glmnet.lasso.cv$lambda.min) 18 x 1 sparse Matrix of class "dgCMatrix" 1 (Intercept) 3332.5402054 Mileage -0.1816504 Cylinder 3634.6147087 Doors -628.9022241 Cruise 340.6710317 Sound 382.0774957 Leather 753.7844280 Buick 924.8954890 Cadillac 13401.5393074 Chevy -482.8713605 Pontiac -1294.4163546 Saab 12273.6389734 Saturn . convertible 11016.0739756 coupe . hatchback -1881.6575830 sedan . wagon 4317.2107830
MSE*3が最小になる lambda の値が18.55です.上の図において,log(lambda) = 3 あたりに点線が縦に引かれていますが,これがminの位置になります.で,真ん中ぐらいにある点線が,lambdaの1se地点の値です.lm() の結果と,lambda.minにおける各係数のあたいをみてみると,微妙に違いがありますね.lassoの場合はwagonではなくsedanが係数0に収束しているようです.
ちなみに,coef() を実行したときにオプションで指定している s というのは,coef を表示する際の lambda の値を指します. cranのドキュメントには,p18の predict.cv.glmnet に
Value(s) of the penalty parameter lambda at which predictions are required. Default
is the value s="lambda.1se" stored on the CV object. Alternatively
s="lambda.min" can be used. If s is numeric, it is taken as the value(s) of
lambda to be used.
と記述されています.
L2正則化
同じように,今度は alpha を0にして,ridge回帰をおこなってみます.
> # ridge > fit.glmnet.ridge <- glmnet(as.matrix(cars[, -1]), + as.matrix(cars[, 1]), + alpha = 0) > plot(fit.glmnet.ridge) > ## cv > fit.glmnet.ridge.cv <- cv.glmnet(as.matrix(cars[, -1]), + as.matrix(cars[, 1]), + nfold = 5, + alpha = 0) > plot(fit.glmnet.ridge.cv) > fit.glmnet.ridge.cv$lambda.min [1] 714.8007 > fit.glmnet.ridge.cv$lambda.1se [1] 1370.924 > coef(fit.glmnet.ridge.cv, s = fit.glmnet.ridge.cv$lambda.min) 18 x 1 sparse Matrix of class "dgCMatrix" 1 (Intercept) 10337.0169783 Mileage -0.1712252 Cylinder 3170.1294044 Doors -831.5817913 Cruise 1026.4850774 Sound 224.6847147 Leather 956.7665236 Buick -1936.7129470 Cadillac 10320.3212670 Chevy -3629.5572140 Pontiac -4111.5436304 Saab 7869.4887792 Saturn -3239.5070500 convertible 9384.0693961 coupe -1729.7150676 hatchback -2962.1017215 sedan -1250.9639471 wagon 2760.2080200
lassoのときとは結果が大きく変わりました.
ElasticNetによる正則化
最後に,ElasticNetを試してみます.基本的には,0 < alpha < 1 であればよいのですが,この alpha の値を決める方法は,{glmnet} 内では提供されていません*4ので,今回はえいやで alpha=0.5 にしちゃいます.ちゃんとやりたいのであれば,{caret} あたりを使って,lambda とalpha を共に変動させてみるのがよいかと思います.
> fit.glmnet.elasticnet.cv <- cv.glmnet(as.matrix(cars[, -1]), + as.matrix(cars[, 1]), + nfold = 5, + alpha = 0.5) > plot(fit.glmnet.elasticnet.cv) > fit.glmnet.elasticnet.cv$lambda.min [1] 33.80277 > fit.glmnet.elasticnet.cv$lambda.1se [1] 416.7364 > coef(fit.glmnet.elasticnet.cv, s = fit.glmnet.elasticnet.cv$lambda.min) 18 x 1 sparse Matrix of class "dgCMatrix" 1 (Intercept) 3864.0228103 Mileage -0.1815926 Cylinder 3625.4650658 Doors -626.2371069 Cruise 371.2344641 Sound 386.8548536 Leather 767.8711841 Buick 402.2514994 Cadillac 12865.1630823 Chevy -1013.4253903 Pontiac -1821.5463454 Saab 11707.2380808 Saturn -464.8502014 convertible 11028.5218995 coupe . hatchback -1877.0655854 sedan -3.3327249 wagon 4323.9610872
ということで,{glmnet} でL1/L2正則化を試してみました.なお,コードはgistにあげてあるので,興味がある方はどうぞ.
*1:単に「正則化 amazon」で検索したら一番上に出てきたのがビショップ本だっただけです.
*2:MiluHatsuneさんのエントリがわかりやすかったので,それをベースになぞってる感じです.
*3:Mean Squared Error,つまり予測値と実際の値の差の二乗和を意味します.
*4:cross validation - Choosing optimal alpha in elastic net logistic regression - Cross Validated