Rで生存時間分析を行う
私事ですが,インフルエンザで1週間くたばっていたせいでR勉強会に参加できませんでした.ただ体調は既にすこぶる回復し,かつ外にも出れなくて暇なので,今まで試したことのなかった生存時間分析を試してみることにしました.
生存時間分析とは
詳しくはwhat_a_dudeさんの解説でまとまっているので参照してくださいなのですが,要するにイベントが発生するまでの時間に影響を与える要因を検討する分析法ですね.もともとは保険数理学の分野で発達し,現在では主に医療統計で使われている手法のようです.典型的なのは,薬剤投与群と非投与群での生存期間の違いをみるといった目的でしょうか.
その中でたぶん一番有名な手法が,コックス比例ハザードモデルというセミノンパラメトリックモデルで,今回はこれを試したいと思います.数理的な理解は,先ほどのページと,あとは土居さんの解説あたりを読むとよいと思います.特徴的なのは,1サンプルに1度しか起きないイベントが生じるまでの時間が目的変数で,かつイベントが観察時間中に生じない場合があることを想定したモデルである(というより,基本的には推定に偏りを与えない),という点でしょうか.
Rでの実施例
サンプルデータ
とりあえずRにもともと入ってるサンプルデータを使うことにします.今回はkidneyデータを使います.このデータは,ポータブル透析装置の利用が,各種腎臓病の患者の生存時間にどう影響するかを検討するための,38ペア(使用と不使用)に対する実験データとなっています(といっても,パラメタにポータブル透析装置の利用有無がないのがよくわからないのですけど...).以下のコマンドを打って,データフレームとして読み込んだ上で最初の部分を出力してみましょう.
> data(kidney) > head(kidney) id time status age sex disease frail 1 1 8 1 28 1 Other 2.3 2 1 16 1 28 1 Other 2.3 3 2 23 1 48 2 GN 1.9 4 2 13 0 48 2 GN 1.9 5 3 22 1 32 1 Other 1.2 6 3 28 1 32 1 Other 1.2
ちなみに各項目の意味は次の通りです.
| 項目 | 意味 |
|---|---|
| patient | ID |
| time | 時間 |
| status | 0:生存(打ち切り),1:死亡 |
| age | 年齢 |
| sex | 男性:1,女性:2 |
| disease | 病気の種類(0:GN, 1:AN, 2:PKD, 3:Other) |
| frail | 元論文からのfrailty推定値 |
コックス比例ハザードモデルの構築
生存時間分析のパッケージを読み込んで,病気の種類による影響をみるモデルを構築します.パラメタ推定法には,直接法、Breslowの近似法、Efronの近似法の3種類が実装されているそうです.こちらの解説によると,近似法の方が計算は簡単だけど,イベント数が多いと推定が不正確になるということのようです.結果は以下の通りです.
> library(survival)
> kidney.cox<-coxph(Surv(time, status)~sex+disease, method="breslow", data=kidney)
> summary(kidney.cox)
Call:
coxph(formula = Surv(time, status) ~ sex + disease, data = kidney,
method = "breslow")
n= 76, number of events= 58
coef exp(coef) se(coef) z Pr(>|z|)
sex -1.4646 0.2312 0.3563 -4.110 3.95e-05 ***
diseaseGN 0.1453 1.1563 0.3630 0.400 0.6890
diseaseAN 0.4195 1.5212 0.3358 1.249 0.2116
diseasePKD -1.3578 0.2572 0.5877 -2.311 0.0209 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
exp(coef) exp(-coef) lower .95 upper .95
sex 0.2312 4.3257 0.1150 0.4648
diseaseGN 1.1563 0.8648 0.5677 2.3554
diseaseAN 1.5212 0.6574 0.7876 2.9378
diseasePKD 0.2572 3.8878 0.0813 0.8138
Concordance= 0.696 (se = 0.045 )
Rsquare= 0.205 (max possible= 0.993 )
Likelihood ratio test= 17.43 on 4 df, p=0.001597
Wald test = 19.52 on 4 df, p=0.0006202
Score (logrank) test = 19.69 on 4 df, p=0.0005759有意な効果があったのは,性別と病気PKDでした.性別のマイナスの効果は,女性(=値が大きい)ほど死ぬ確率(=ハザードが起こる確率)が低い(=値が小さい)ということのようです.
モデルの仮定が成り立っているかを確認
コックス比例ハザードモデルでは,共変量の効果は時間によらず一定である,という仮定をおいています.つまり,性別の効果が最初は小さいが,時間の経過とともにどんどん大きくなっていく,といった場合には,当該変数がモデルの仮定を満たしていないと考えられる訳です.その検定は以下のように実施します.
> kidney.coxzph <- cox.zph(kidney.cox)
> kidney.coxzph
rho chisq p
sex 0.18839 2.60676 0.106
diseaseGN -0.01392 0.01123 0.916
diseaseAN 0.06162 0.20036 0.654
diseasePKD 0.00701 0.00438 0.947
GLOBAL NA 4.20781 0.379
> par(mfrow=c(2, 2))
> plot(kidney.coxzph, df=2)
この場合,どれも上記仮定をきちんと満たしているようにもみえないですが,性別に関しては有意水準10%にギリギリ引っかからない程度で,それほどひどく仮定から逸脱している訳でもなさそうです.ここでは細かい点は無視して,手法の確認を続けます.
Kaplan-Meier曲線の記述
さて,さきほど作ったモデルをグラフに表してみましょう.生存時間分析においては,生存確率の時間変化を記述したグラフである,Kaplan-Meier曲線というのが代表的な記述法とのことですので,これを出力してみます.
kidney.fit <- survfit(kidney.cox) plot(kidney.fit)

95%信頼区間を表示して,生存確率の時間変化を記述できました.また打ち切りデータについてはこの中の+で表されています.なお,先ほどの病気ごとの違いのように,群ごとの違いをみたい場合には,直接式を打ち込んであげます.
kidney.fit <- survfit(Surv(time, status)~disease, data=kidney)
plot(kidney.fit, xlab='Time', ylab='Survival Rate', col=c('red', 'green', 'blue', 'black'))
legend(300, 0.8, legend=c('Other', 'GN', 'AN', 'PKD'), lty=1, col=c('red', 'green', 'blue', 'black'))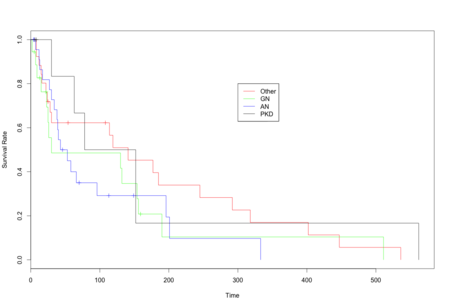
なお,2群以上の結果を表示させた場合には,デフォルトでは信頼区間の表示がオフになります.これをおんにしたいときには,以下のようにオプションをつけてあげます.
plot(kidney.fit, conf.int=TRUE, xlab='Time', ylab='Survival Rate', col=c('red', 'green', 'blue', 'black'))
Log-Rank検定の実施
上記のように,2群以上の観測値が得られたときに,この群ごとの差を検定する打表的な手法がLog-Rank検定です.これを実施するには,以下のようにコマンドを記述します.ここでは,先ほど有意な効果がみられた性別について実際に検定をしてみましょう.
> kidney.lr.sex <- survdiff(Surv(time, status)~sex, subset=(sex %in% c("1", "2")), data=kidney)
> kidney.lr.sex
Call:
survdiff(formula = Surv(time, status) ~ sex, data = kidney, subset = (sex %in%
c("1", "2")))
N Observed Expected (O-E)^2/E (O-E)^2/V
sex=1 20 18 10.2 5.99 8.31
sex=2 56 40 47.8 1.28 8.31
Chisq= 8.3 on 1 degrees of freedom, p= 0.00395一般的によく使われる5%有意水準を用いたら,ここではp=約0.4%で5%より小さいので,女性(sex=2)のほうが長く生存するといえるでしょう.
以上,ざっとコックス比例ハザードモデルの手法についてみてきました.このモデルは,例えば会員離脱なんかの予測にも使えそうですね.いろいろ応用の利く場面がありそうです.