中古マンション売買データを分析してみた(2.4) - 個体差を入れた階層ベイズモデルへの拡張
引き続きStanでモデルの拡張を行っていきます.前々回の結果について,通常の線形モデルをStanで回したわけですが,順調にこれを拡張していきます.まずは個体差のランダム効果項を入れて,よりモデルの汎化性を高めていきたいと思います.階層ベイズについては,TJOさんの解説記事が既にあるので,詳細について私の方であれこれいう必要はなさそうです.粛々とモデルを組めばよろしいかと思われます.
モデルの拡張
今回の形では,各物件が1サンプルに該当します.物件毎の個別の動きというものをランダム効果として切り離した上で,主たる独立変数の効果を改めて確認しよう,というのが今回の趣旨になります.早速ですが,Stanコードは以下のようになります*1*2.
線形モデルとの違いは,全サンプルの個体差を表すランダム効果項の]と,その分散を表す
がパラメタに追加されたところです.ランダム効果項については,期待値はゼロ,分散を決めるパラメタ
については無情報事前分布として,一様分布を事前分布として設定します.なお,切片
については,もともとの
の期待値を初期値として与えました.
data { int<lower=1> N; int<lower=1> M; matrix[N, M] X; vector[N] Y; } parameters { real a; vector[M] b; real r[N]; real<lower=0> s; real<lower=0> s_r; } model { # regresion model with random effect for (i in 1:N) Y[i] ~ normal(a+X[i]*b+r[i], s); # prior distributions s ~ uniform(0, 1.0e+4); a ~ normal(39, 1.0e+4); for (i in 1:M) b[i] ~ normal(0, 1.0e+4); for (i in 1:N) r[i] ~ normal(0, 1/(s_r*s_r)); # hierarchical prior distribution s_r ~ uniform(0, 1.0e+4); }
シミュレーションの実行と結果
収束までのプロット
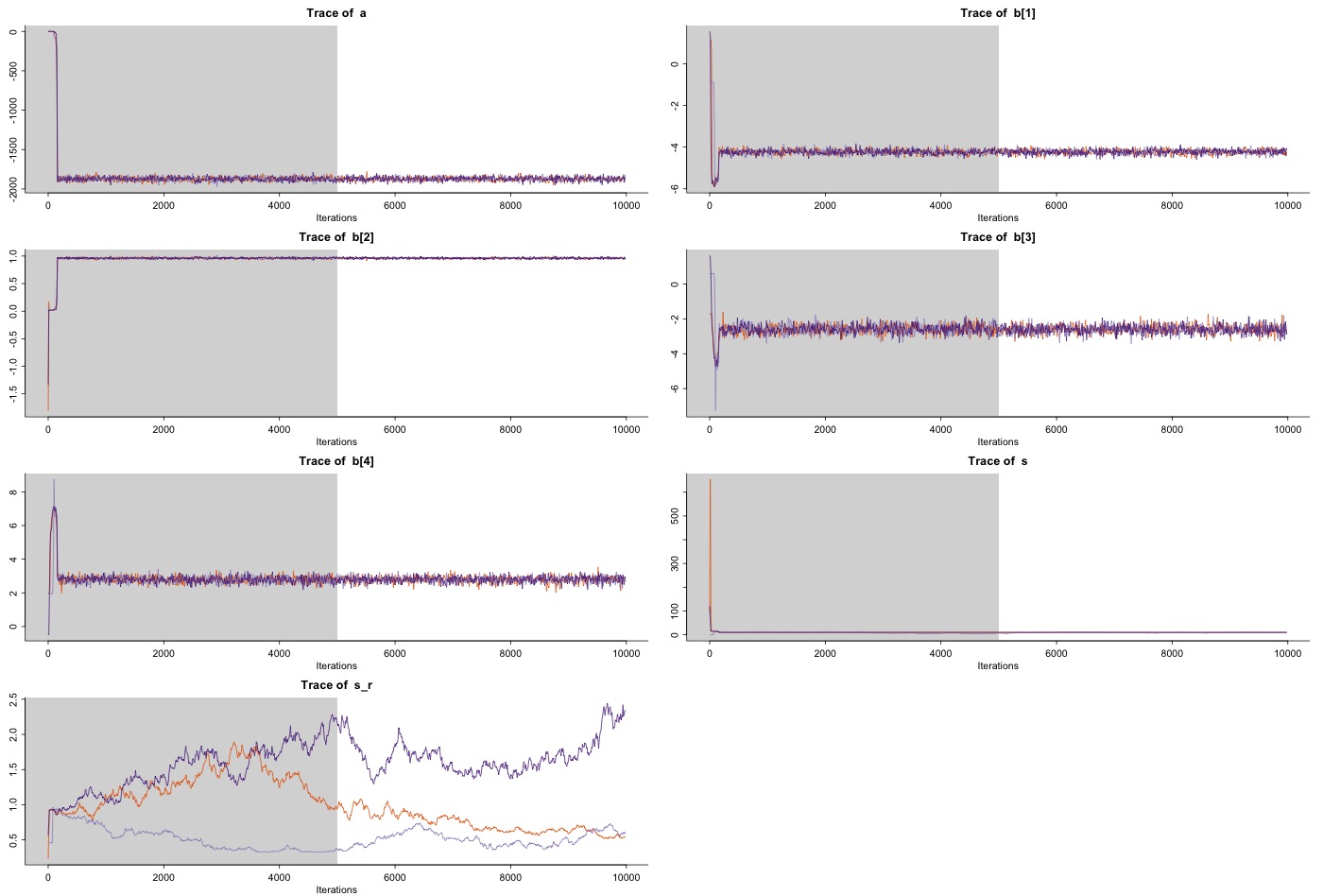
そして,Stanのイテレーションを10000回,burn-inを5000回として,3 chain,10 thinで回しました*3*4.収束までのプロットをみると,以下のようになっていて,おおむね問題なく収束しているように思えます.というか,300ステップくらいでほぼ収束しているように見えるので,たぶん10000 iterも回す必要なかったですね.
ただ個体差のについては,ある程度分散が収束しないのは仕方がないのかもしれないですね... というより,ここの部分はきちんと収束するものなんでしょうか? というのが自分の中でも疑問...
細かいところですが,今回の推定だと4800以上のサンプルすべてについてが推定されてしまうため,そのままサマリを出したり,プロットしたりすると悲劇が待っています.そんなときは以下のように,必要な変数だけを指定してあげるとカオスのような結果にならなくて住みます.
# print summary print(model.fit, digits_summary=2, pars=c('a', 'b', 's', 's_r')) # draw traceplot traceplot(model.fit, pars=c('a', 'b', 's', 's_r'))
線形モデルとの比較
以下の両者を見比べればわかるように,推定値はほとんど変わりません.各パーセンタイルをみても,ほぼ問題なさそうといえるのではないでしょうか.ということで,今回のデータについては個体差が悪さをしているということはほぼなさそうに思えますね.
階層ベイズモデル
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat a -1871.89 0.70 26.41 -1922.04 -1889.75 -1871.94 -1854.13 -1820.61 1412 1.00 b[1] -4.23 0.00 0.12 -4.48 -4.31 -4.22 -4.14 -4.00 1500 1.00 b[2] 0.96 0.00 0.01 0.94 0.95 0.96 0.97 0.99 1408 1.00 b[3] -2.60 0.01 0.25 -3.07 -2.77 -2.61 -2.44 -2.13 1500 1.00 b[4] 2.79 0.01 0.19 2.40 2.67 2.81 2.92 3.16 1426 1.00 s 9.60 0.42 0.75 7.24 9.52 9.87 10.02 10.21 3 1.39 s_r 0.98 0.43 0.55 0.38 0.56 0.70 1.52 2.19 2 3.68
線形モデル
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat alpha -1873.43 0.36 26.97 -1926.05 -1891.81 -1873.25 -1855.43 -1820.64 5767 1 beta[1] -4.23 0.00 0.12 -4.47 -4.31 -4.23 -4.15 -4.00 9278 1 beta[2] 0.96 0.00 0.01 0.94 0.95 0.96 0.97 0.99 5765 1 beta[3] -2.60 0.00 0.25 -3.10 -2.77 -2.60 -2.43 -2.11 7327 1 beta[4] 2.79 0.00 0.20 2.40 2.66 2.79 2.92 3.18 6920 1 sigma 10.07 0.00 0.10 9.87 10.00 10.07 10.14 10.27 10643 1 lp__ -13553.97 0.02 1.73 -13558.15 -13554.89 -13553.67 -13552.71 -13551.58 5047 1
次のステップ
ということで,ここまで拡張したところで,次はようやく駅と路線の効果を入れていきたいと思います.ある程度モデルが固まったら,改めて(3)にしてまとめたいところですね...
*1:どうでもいいんですが,はてなのコードブロックでは,Rのカラースキームはありますが,Stanのはまだ存在していません.早めにサポートしてもらえるとうれしいとは思っていますが,流石にまだ認知度低すぎですからね...
*2:ちなみにVimにはStanのカラースキームが普通に存在しており,maverickg/stan.vim · GitHubから入手できます.RStudioでもStanのカラースキームやシンタックス補完はサポートしていないので,地味に便利です.
*3:シミュレーションにかかった時間については正確に計測していないのでアレですが,昼過ぎに回し始めて,次の日の朝起きたら終わっていたので,せいぜい15時間くらいなのかなーという予想です.次からはちゃんと時間を計測しよう... ちなみに@beroberoさんのエントリ RStanの並列化と後処理・ggplotの例 を参考に,doParallelを使って3 chainを並列で回していて,この時間がかかっています.Core i7の2.3GHzクアッドコア使っているんですけどね...