中古マンション売買データを分析してみた(2.1) - MCMCで線形モデルを推定するためのパラメタ設定はどうすればいいか
今回のエントリはテクニカルな問題のお話のみで,住宅価格についての蘊蓄はいっさい含まれておりません.統計モデリングに興味のある方のみお読みください.
問題
前回のモデルでは,単純に群間の差を駅,路線の2層の群を使ってモデリングしました.考察のところでも書いたように,実のところあのモデルは余りよろしくないわけです.なにかといったら,前々回のモデリングで使っており,有用であることがわかっている駅からの距離,築年数という変数を使っておらず,そのため推定結果にバイアスがかかっていました*1.じゃあやれよ,という話になりますが,実際には,やってみた上でパラメタ収束が劣悪だったため,モデルに組み込むのをあきらめたという経緯があります.
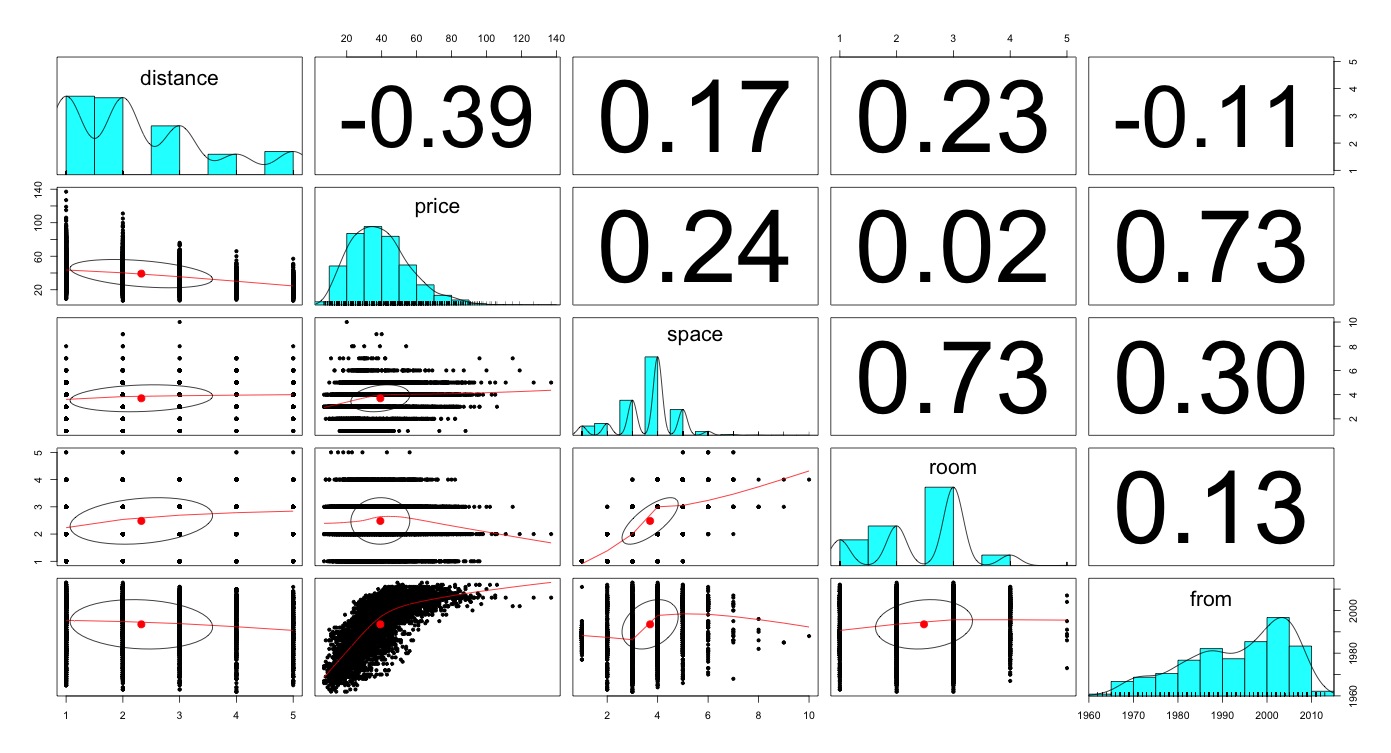
しかし,普通にlm()で導出した線形回帰でも,十分に有意な値が出ているし,分布形状をみてもそこまで当てはまりが悪いとは考えにくいわけです(もちろん厳密には正規分布近似が妥当か? というような形状であることは否定しませんが...).
分析結果
lm()による最小二乗法推定
lm()を使って推定した結果が以下になります.全体的にモデルの当てはまりはそれなりで,まぁ悪くない数字なのではないかと思います,
> summary(lm(price~space+room+distance+from, data=d)) Call: lm(formula = price ~ space + room + distance + from, data = d) Residuals: Min 1Q Median 3Q Max -30.449 -6.879 -0.793 5.841 75.247 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -1.873e+03 2.667e+01 -70.23 <2e-16 *** space 2.796e+00 1.987e-01 14.07 <2e-16 *** room -2.608e+00 2.510e-01 -10.39 <2e-16 *** distance -4.230e+00 1.200e-01 -35.24 <2e-16 *** from 9.623e-01 1.343e-02 71.63 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 10.06 on 4821 degrees of freedom Multiple R-squared: 0.6451, Adjusted R-squared: 0.6448 F-statistic: 2190 on 4 and 4821 DF, p-value: < 2.2e-16
JAGSによるMCMC推定
1500 iteration, 100 burn-in, 3 thin*2
さて,これを同様にJAGSを使って推定してみます.もちろんこんな単純なモデルをMCMC推定する意味は全くないのですが,この先に一般化線形混合モデル,階層ベイズモデルに展開することを考えているため,まずはシンプルなモデルをJAGSで組むことにしたわけです.コードは以下の通りです*3.
# mcmc modeling ## model description mantion_model <- function() { # main model for (i in 1:N) { PRICE[i] ~ dnorm(b+bD*DISTANCE[i]+bF*FROM[i]+bR*ROOM[i]+bS*SPACE[i], tau[1]) } # prior distribution b ~ dnorm(0.0, 1.0e-6); bD ~ dnorm(0.0, tau[2]); bF ~ dnorm(0.0, tau[3]); bR ~ dnorm(0.0, tau[3]); bS ~ dnorm(0.0, tau[4]); for (i in 1:N.tau) { tau[i] <- 1 / (sigma[i] * sigma[i]) sigma[i] ~ dunif(0.0, 1.0e+6) } } # モデルの書き出し先 file.bugs <- file.path('script/mantion.bug') R2WinBUGS::write.model(mantion_model, file.bugs) # data for JAGS list.data <- list( PRICE = d$price, DISTANCE = d$distance, FROM = d$from, ROOM = d$room, SPACE = d$space, N = nrow(d), N.tau = 4 ) # initial value for JAGS inits <- list( b = rnorm(1, 39.22, 16.88), bD = rnorm(1, 0, 100), bF = rnorm(1, 0, 100), bR = rnorm(1, 0, 100), bS = rnorm(1, 0, 100), sigma = runif(4, 0, 100) ) # estimate parameter params <- c('b', 'bD', 'bF', 'bR', 'bS', 'sigma') # model definition model <- jags.model( file = file.bugs, data = list.data, inits = list(inits, inits, inits), n.chain = 3 ) # set MCMC burn-in cycles update(model, 100) # conduct MCMC silumation results post.list <- coda.samples( model, params, thin = 3, n.iter = 1500 ) plot(post.list)
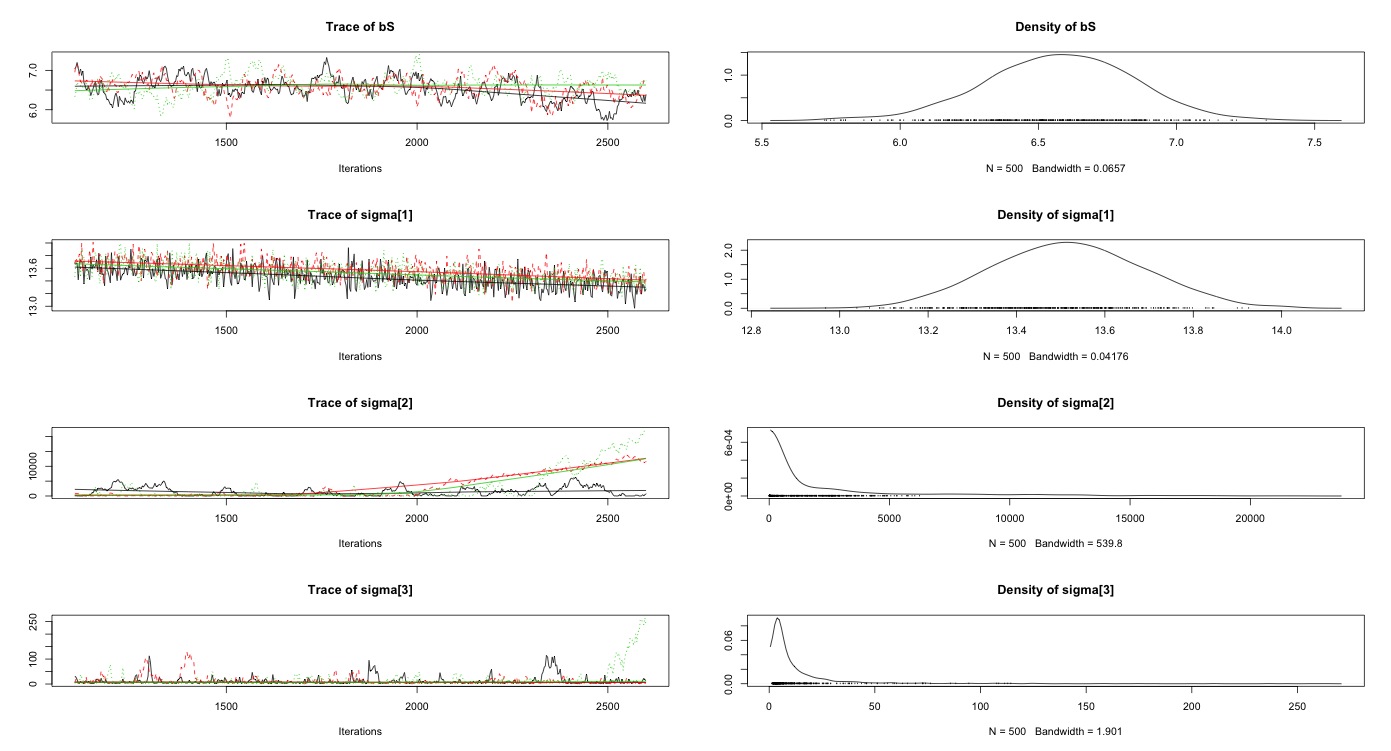
推定結果のプロットを行うと,全く推定結果が収束していないのが見て取れるかと思います.特に切片と築年が酷いことになっています.ちゃんと理解できていないのですが,これってMCMCのイテレーションをもっとずっと増やせば安定するんですかね? 100万回とか...
実際に各パラメタ推定におけるR-hatを確認して,収束診断をしてみましょう.JAGSではR-hatを確認できないのですが,@beroberoさんに教えていただいたやり方で,WinBUGSパッケージのオブジェクトに変換してR-hatを確認することができます.やはりbとbFの収束が1.5と悪いことが見て取れます.
推定された各回帰係数も,最小二乗法とは大きく異なっているので,いろいろとアレな感じがしますね.とりあえず,もう少し収束っぽくなるまで計算回し続けてみますか...
# convert to BUGS object mcmc.list2bugs <- function(mcmc.list) { b1 <- mcmc.list[[1]] m1 <- as.matrix(b1) mall <- matrix(numeric(0), 0, ncol(m1)) n.chains <- length(mcmc.list) for (i in 1:n.chains) { mall <- rbind(mall, as.matrix(mcmc.list[[i]])) } sims.array <- array(mall, dim = c(nrow(m1), n.chains, ncol(m1))) dimnames(sims.array) <- list(NULL, NULL, colnames(m1)) mcpar <- attr(b1, "mcpar") as.bugs.array( sims.array = sims.array, model.file = NULL, program = NULL, DIC = FALSE, DICOutput = NULL, n.iter = mcpar[2], n.burnin = mcpar[1] - mcpar[3], n.thin = mcpar[3] ) }
> mcmc.list2bugs(post.list) 3 chains, each with 2600 iterations (first 1100 discarded), n.thin = 3 n.sims = 1500 iterations saved mean sd 2.5% 25% 50% 75% 97.5% Rhat n.eff b -211.5 26.8 -264.8 -232.6 -210.0 -191.1 -161.7 1.5 7 bD -5.5 0.2 -5.8 -5.6 -5.5 -5.4 -5.1 1.0 110 bF 0.1 0.0 0.1 0.1 0.1 0.1 0.2 1.5 7 bR -4.2 0.3 -4.8 -4.4 -4.2 -4.0 -3.5 1.0 76 bS 6.6 0.3 6.0 6.4 6.6 6.8 7.1 1.0 110 sigma[1] 13.5 0.2 13.2 13.4 13.5 13.6 13.8 1.1 26 sigma[2] 2568.7 4074.1 5.0 49.4 569.9 2995.7 15165.5 1.0 250 sigma[3] 14.9 27.4 1.8 3.6 6.1 14.0 95.2 1.0 460 sigma[4] 5500.0 10019.8 6.4 98.0 1079.4 6296.9 41095.6 1.1 50 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
100000 iteration, 100 burn-in, 3 thin
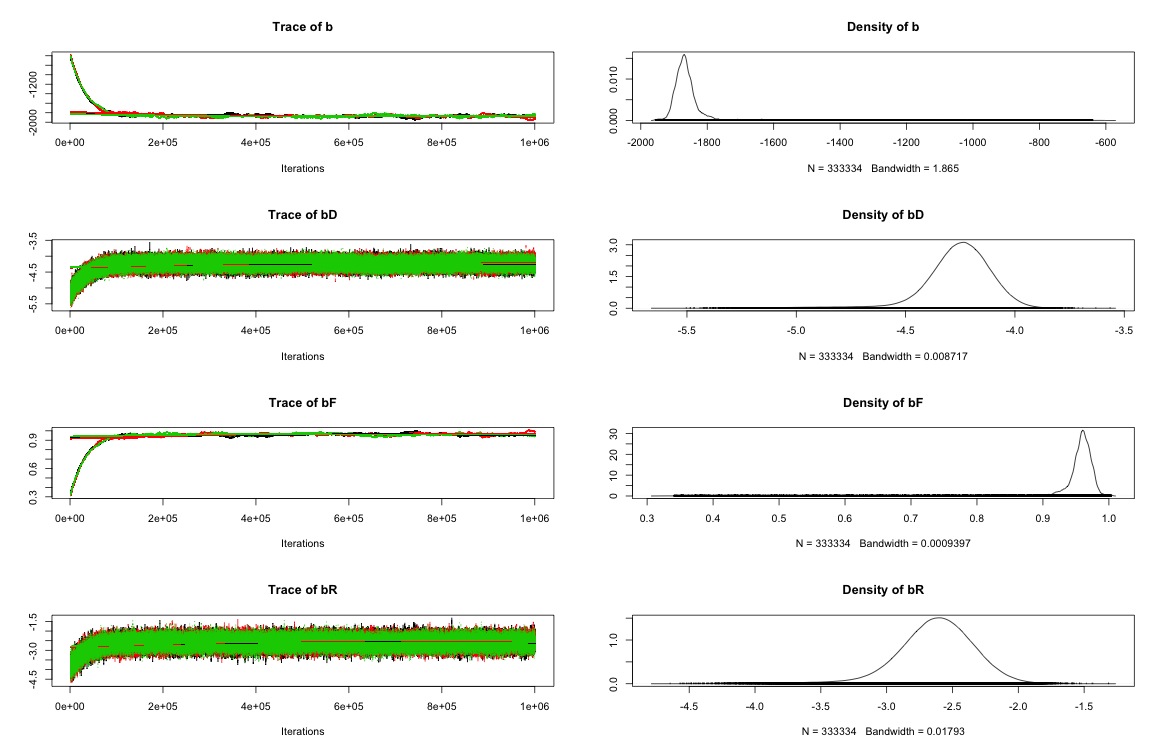
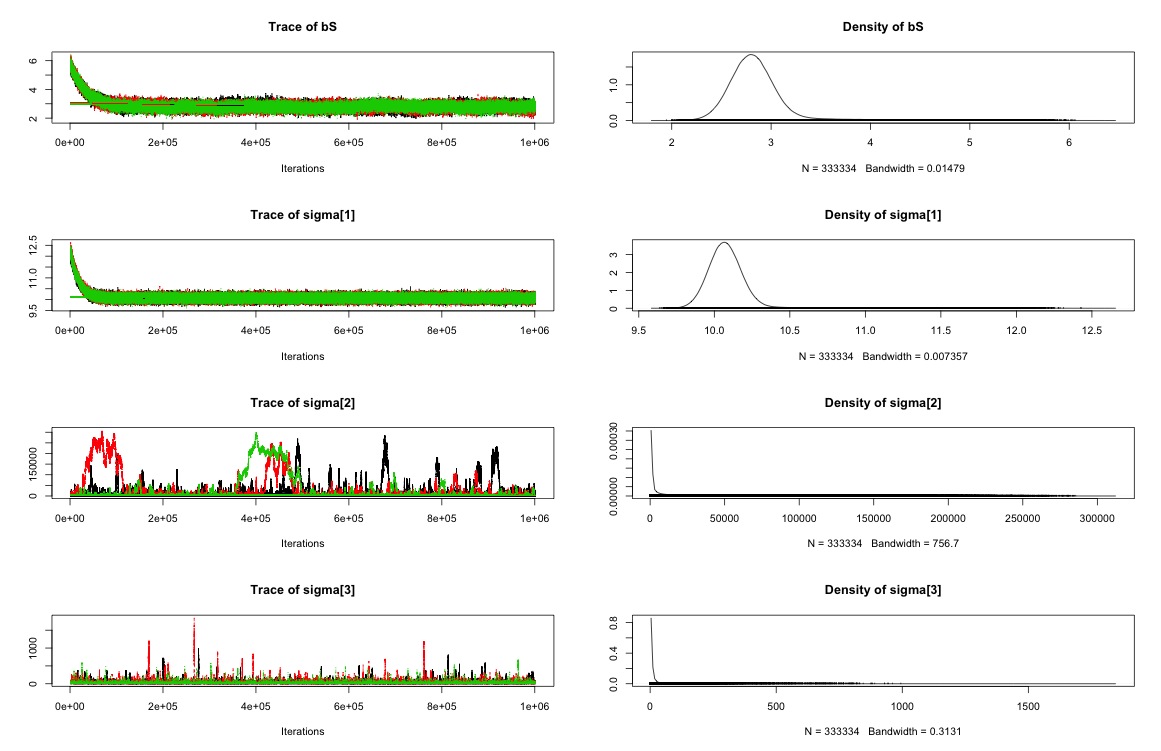
先ほどのシミュレーションだと,bとbFの傾きが変化し続けている状態で,明らかにまだ収束に至っていなさそうだったので,イテレーション回数を増やして再計算することにしました.3回まわしで各10万イテレーションにして計算しなおしたところ,今度はおおむね収束したといえそうな形になりました.値もおおむねlm()のときと一致しており,妥当な形になったといえそうです.実際に収束に至るまでには,だいたい2万イテレーションぐらいあれば良かったみたいですね.まぁイテレーション回し終わるのに6時間くらいかかりましたが...
> mcmc.list2bugs(post.list) 3 chains, each with 1001102 iterations (first 1100 discarded), n.thin = 3 n.sims = 1000002 iterations saved mean sd 2.5% 25% 50% 75% 97.5% Rhat n.eff b -1830.4 159.7 -1915.0 -1884.2 -1867.2 -1846.9 -1267.3 1 11000 bD -4.3 0.2 -4.7 -4.3 -4.2 -4.2 -4.0 1 20000 bF 0.9 0.1 0.7 0.9 1.0 1.0 1.0 1 22000 bR -2.6 0.3 -3.3 -2.8 -2.6 -2.4 -2.1 1 94000 bS 2.9 0.4 2.4 2.7 2.8 3.0 4.2 1 10000 sigma[1] 10.1 0.2 9.9 10.0 10.1 10.1 10.6 1 60000 sigma[2] 26003.6 56848.5 4.2 62.6 970.6 15224.3 216815.1 1 400 sigma[3] 13.2 47.1 1.2 2.4 4.1 8.7 79.7 1 8300 sigma[4] 24431.4 46458.6 3.0 55.7 1129.1 23171.6 161349.9 1 86 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
80000 iteration, 20000 bunr-in, 40 thin
ということで,今度は値が変化している状態の不安定なパラメタをburn-inに入れてしまって,さらに間引きも40にして計算を軽くしてみたいと思います.そうすると,上の場合とそれほどは変わらない値が得られ,かつ計算時間も2時間程度とだいぶ高速化されました.ただbのR-hatがまだ1.1というところをみて,もう少し間引き数を減らすかステップ数を増やすかの対応が必要そうです.
> mcmc.list2bugs(post.list) 3 chains, each with 101000 iterations (first 21000 discarded), n.thin = 40 n.sims = 6000 iterations saved mean sd 2.5% 25% 50% 75% 97.5% Rhat n.eff b -1712.2 91.0 -1829.2 -1790.2 -1739.4 -1653.5 -1517.0 1.1 50 bD -4.4 0.1 -4.6 -4.4 -4.4 -4.3 -4.1 1.0 220 bF 0.9 0.0 0.8 0.9 0.9 0.9 0.9 1.0 52 bR -2.8 0.3 -3.3 -2.9 -2.8 -2.6 -2.3 1.0 340 bS 3.2 0.3 2.7 3.0 3.1 3.3 3.8 1.0 81 sigma[1] 10.1 0.1 9.9 10.0 10.1 10.2 10.3 1.0 440 sigma[2] 493966.3 289142.0 20444.8 244921.5 488970.6 745387.6 973813.5 1.0 6000 sigma[3] 496396.3 284594.6 25977.7 252167.8 493177.6 739757.1 974007.0 1.0 6000 sigma[4] 498123.5 288435.7 22577.8 245519.2 502556.0 749505.3 972328.5 1.0 5100 sigma[5] 505126.8 289866.8 25836.7 251756.4 507867.7 760266.6 976506.2 1.0 6000 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
ということで
自分の理解があやふやなのに問題があるのはわかっているわけですが,とりあえず試行錯誤の過程を公開しておくことにします.引き続き精進していきます.最後に,アホとしてこちらのメッセージを胸に刻んでおきたいと思います.高々線形回帰するだけで6時間計算にかけてるようじゃね...Stan使わないとこれ以上の処理は無理なのでは感.
久保本に言ってることは、端的にいえば、初心者に最小二乗法とかランダム効果モデルとか教える必要なし、最初から最尤法、階層ベイズモデルでいいじゃない、ということだと思うよ。概念がウリというのはそういうこと。ただ計算法は別で、なんでもMCMCでやる人がいたらそれはアホ。
— baibai (@ibaibabaibai) 2014, 5月 30